Lanzamiento Inclinado
El lanzamiento inclinado puede considerarse como la integración del movimiento rectilíneo uniforme
y el lanzamiento vertical en sus dos momentos, ascendente al inicio y descendente luego de llegar a su altura máxima. Debido a esto posee una componente vertical y una horizontal de distancia y velocidad, teniendo en común el tiempo y manteniendo una aceleración vertical constante por la acción de la gravedad (horizontalmente no existe aceleración en este movimiento puesto que es MRU).
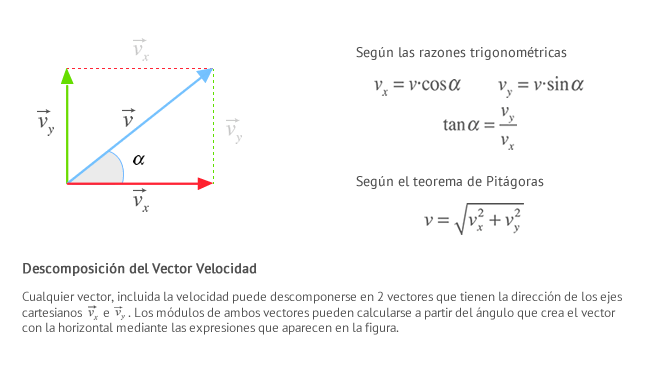
Como el movimiento se ve influenciado por el ángulo con que es lanzado el cuerpo las componentes de velocidad tanto vertical como horizontal vienen dadas por:

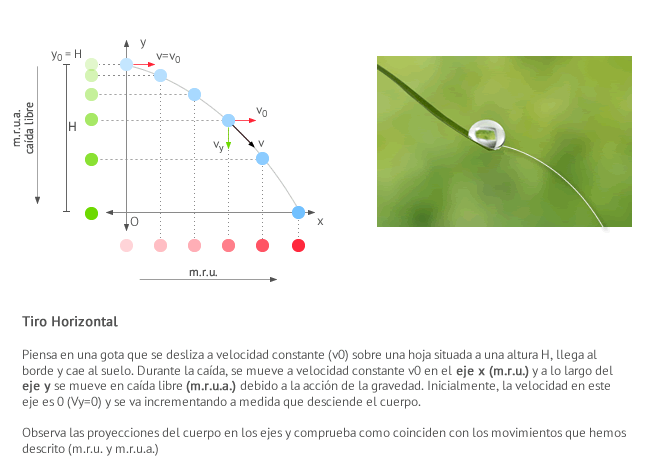
Lanzamiento Horizontal
Una pelota de béisbol se proyecta horizontalmente en el vacío desde un punto O con velocidad . Si la tierra no ejerciera ninguna atracción sobre la pelota, y se supone nulara resistencia del aire, la pelota se movería en el vacío y en tiempos t1,t2,t3?
ocuparía posiciones tales como A, B, C, D ,?
y el movimiento sería rectilíneo uniforme de velocidad constante . Sin embargo como la pelota está sometida a la atracción gravitatoria, a la vez que se mueve horizontalmente, cae verticalmente con aceleración constante - y al final de los tiempos indicados, las posiciones de la pelota son,respectivamente, A', B',C',D',? la curva que une a estos puntos corresponde a una Parábola.
Ecuaciones
Las ecuaciones del lanzamiento horizontal son:
* Las ecuaciones del m.r.u. para el eje x
x=x0+vx⋅t
* Las ecuaciones del m.r.u.a. para el eje y
vy=v0y+ay⋅t
y=y0+v0y⋅t+12⋅ay⋅t2
Dado que, como dijimos anteriormente, la velocidad forma un ángulo α con la horizontal, las componentes x e y se determinan recurriendo a las relaciones trigonométricas más habituales:
Lanzamiento Ascendente
Un cuerpo lanzado verticalmente hacia arriba se mueve con movimiento uniformemente retardado hasta que su velocidad sea igual a cero, a esto se le conoce como lanzamiento vertical hacia arriba. En este momento el cuerpo alcanza mayor altura y empieza a caer libremente de esta altura moviéndose de nuevo hacia abajo debido a la fuerza de gravedad.
CARACTERÍSTICAS DEL LANZAMIENTO VERTICAL HACIA ARRIBA:
La trayectoria del movimiento es lineal.
El cuerpo regresa al punto de partida por la misma vertical.
Para poder subir el cuerpo necesita velocidad inicial.
Mientras sube, la aceleración de la gravedad actúa en sentido opuesto al de la velocidad, el movimiento es uniformemente retardado (ten en cuenta que en este movimiento se usa signo negativo).
Mientras baja, la aceleración de la gravedad actúa en el mismo sentido a la de la velocidad, el movimiento es uniformemente acelerado (ten en cuenta que en este movimiento se usa signo positivo).
La rapidez con que se inicia el movimiento es la misma con que termina en el punto de partida.
El tiempo que tarda en subir es el mismo tiempo que emplea para llegar desde la altura máxima hasta el punto de partida.
En la altura máxima es cero, por eso, comienza allí a descender.
Tiempo máximo es el empleado para llegar al punto mas alto de la trayectoria donde la velocidad es cero.
Tiempo de vuelo es el empleado que llega a la altura máxima mas el tiempo empleado desde la altura máxima hasta el punto de partida.
ECUACIONES:
Las ecuaciones del lanzamiento vertical son las mismas del movimiento uniformemente variado retardado, por lo tanto la aceleración de la gravedad toma como valor negativo
Si la velocidad inicial es diferente a cero:
Vf² = Vo² + 2 • g • y
Vf =Vo + g • y
Y =Vo • t + g • t² / 2
Si la velocidad inicial es igual a 0, las ecuaciones quedarían así:
Vf² = 2 •g • y
Vf = g • t
Y = g • t² / 2
Para tiempo y altura máxima:
Ymax = -Vo²/2 • g
Tmax = -Vo/ g
---------------------------------------------------------------------------
Vf = Velocidad final
Vo = Velocidad inicial
g = Gravedad (9.8 m/seg²)
Y = Altura
t = Tiempo
Tmax = Tiempo máximo
Ymax = Altura máxima
me encantan que estos contenidos ayudan a muchos estudiantes como yo, porque encuentro rápidamente la ayuda graciasssssss
ResponderBorrarGran post, exelente! Thx
ResponderBorrarexelente post !! de mucha utilidad
ResponderBorrarnepe
ResponderBorrargracias me sirvio el contenido
ResponderBorrarNo entendí pero igual me sirve 😁
ResponderBorrarawebOooOOooOOOOOUUuuuUUUuuuU
ResponderBorrar